Longda's Interesting World

Longda's Interesting World

《数据库实现》-- 第三章 索引

《数据库实现》-- 第三章 索引

第三章 索引

索引结构基础

索引的数据文件， 必须建立索引和记录之间的关联， 索引的指针指向的记录必须含索引对应的值。
索引如果是稠密的， 则为每个记录设一个索引。
当索引是稀疏的， 则需要主索引和辅助索引。 

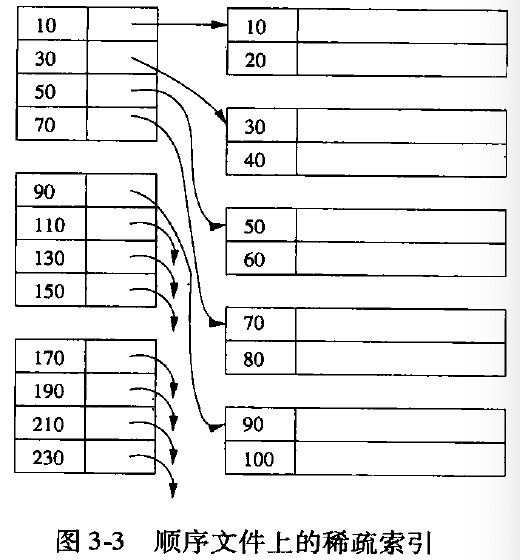
顺序文件

按照主键进行排序生成的文件。 表中的元祖按照这个次序分布在多个数据块中。

稠密索引

当索引文件索引块保持键的顺序和数据文件中排序一直。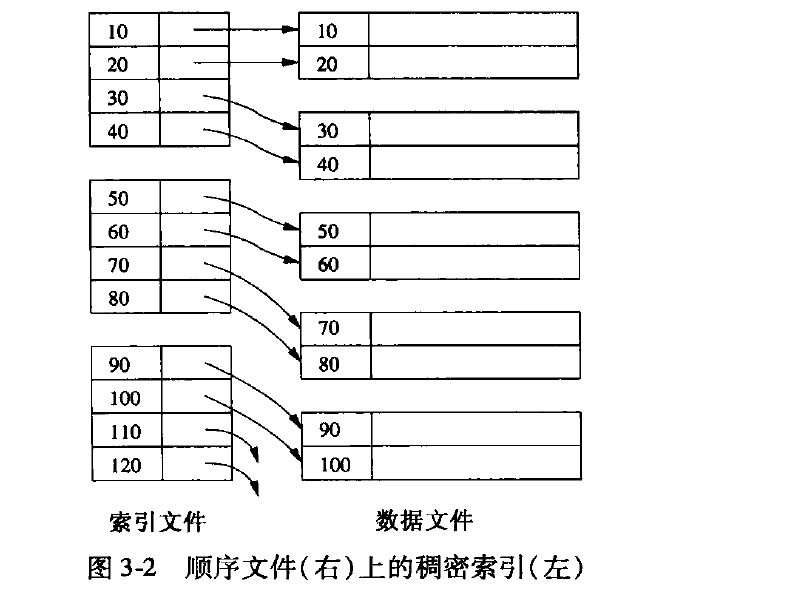 
image.png

这种方式， 因为索引是排序的，可以用二分查找来加速查找， 另外， 因为索引的数据量小，可以完全被load到内存中。 

稀疏索引

这个里面有一个条件， 数据文件必须是按照查找键进行排序。 
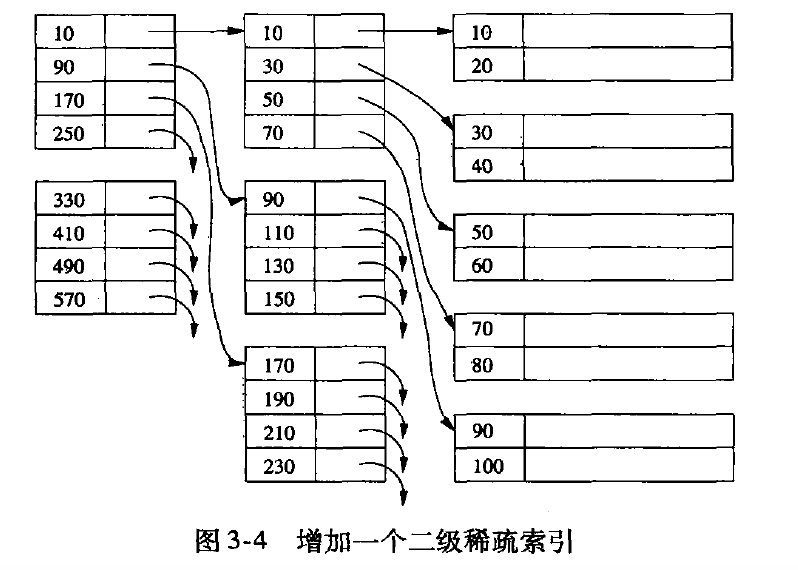
image.png

多级索引

image.png
类似上图， 但多级索引效率依旧比较低，因此更常规的做法是使用b+树。

辅助索引（非主键索引）

辅助索引表示索引键的排序和数据文件的排序是不同的， 因此必须是稠密索引， 因此稀疏索引是毫无意义。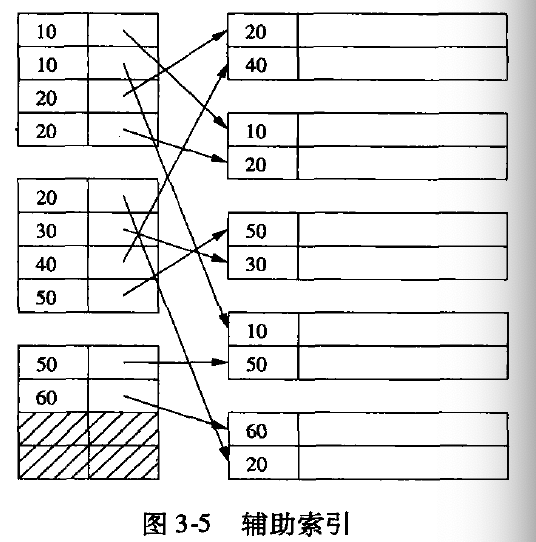
image.png
因为索引键非唯一性， 因此，对一个值进行查找时， 可能还是会查找多个数据文件的块。
辅助索引一种用途就是做聚集文件， 比如表r 和s， r 中多条记录对于s中一条记录。
比如
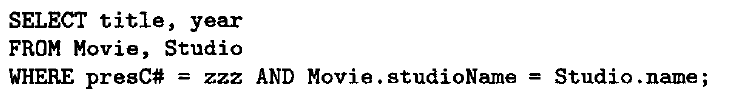
image.png
image.png
基于studioname 和pressc# 建立一个聚集文件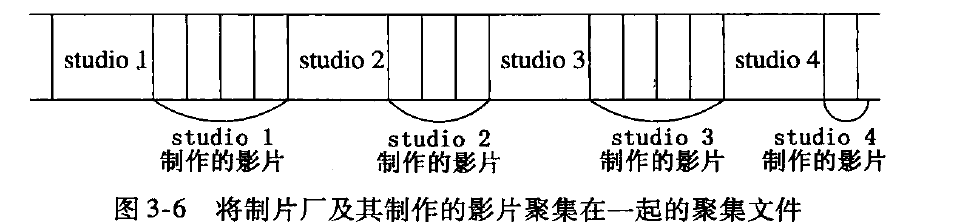
image.png

辅助索引的间接层

当辅助索引重复率非常高时， 索引文件的效率比较低，可以引入一个间接索引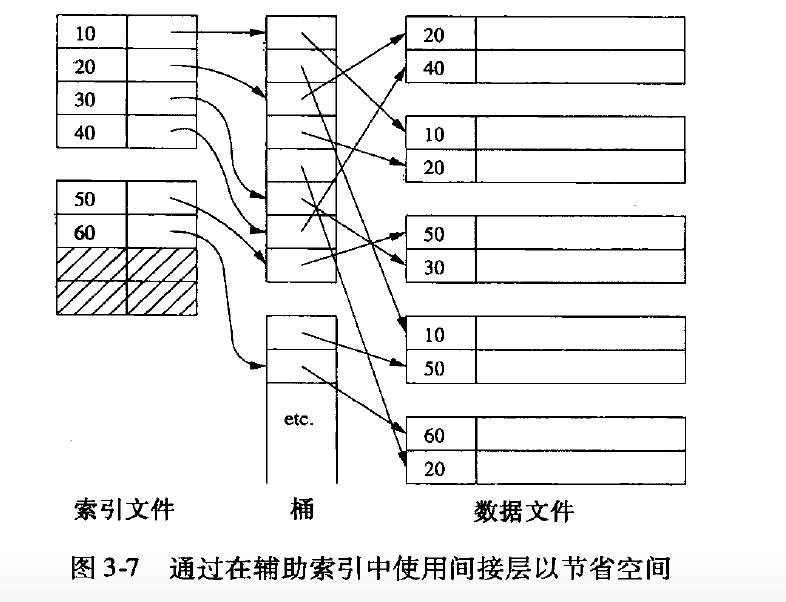
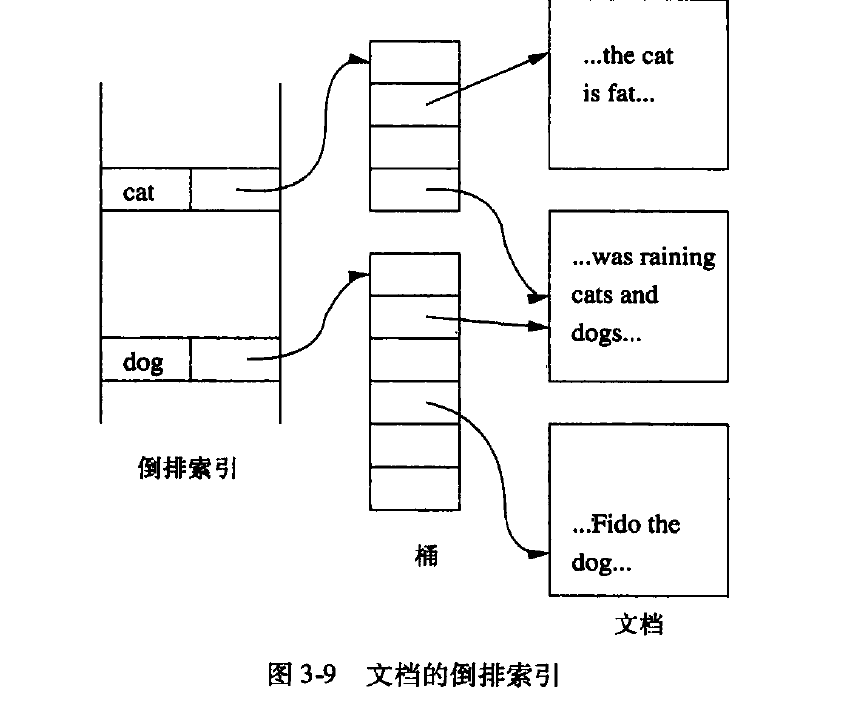
image.png

倒排索引

  • 一个文档可以被看作是doc 的一个元组
  • 每个元组类似doc(hascat, hasdog, hascar…), 每个属性表示文档含有该关键字
  • 关系doc 上为每个属性建立一个辅助索引， 只需为出现该关键字的文档建索引
  • 不是为每个属性建一个索引，而是把所有的索引合成一个，称为倒排索引。 
  • image.png

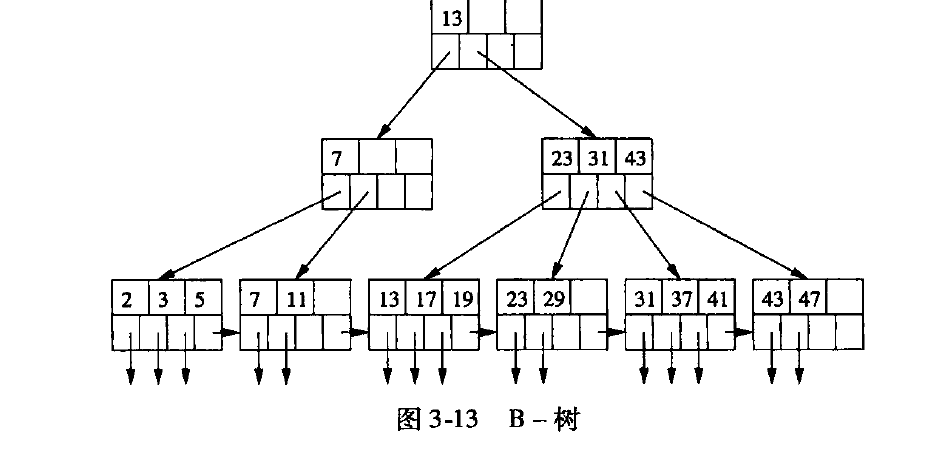
b- 树

  • 平衡二叉树， 每个块都处在半满和全满之间
  • 根， 至少被2个节点使用
  • 叶节点中， 最后一个指针指向下一个叶节点的存储块
  • 内层节点， 含有n+1个指针指向下一层的块， 摒弃[(n+1)/2]  个指针被使用了。 如果含有j个指针，则含有j-1个键， 为k1, k2, k3, …, k(j-1). 第一个指针指向小于k1的块， 第二个指针指向k1《=v 《 k2
  • 所有的键和指针，存放在数据块的头部。 
  • image.png
  • b- 树是数据文件的主键， 索引是稠密的， 数据文件可以不按主键排序
  • 当数据文件按主键排序，且b+树是稀疏索引， 则叶节点为数据文件每一个块设一个键-指针对
  • 当数据文件按主键排序，但b+ 树属性非主键。 则索引是稠密的，叶节点为每个属性都设置键-指针对，k指向第一个记录。
  • b-树可扩展带重复。 

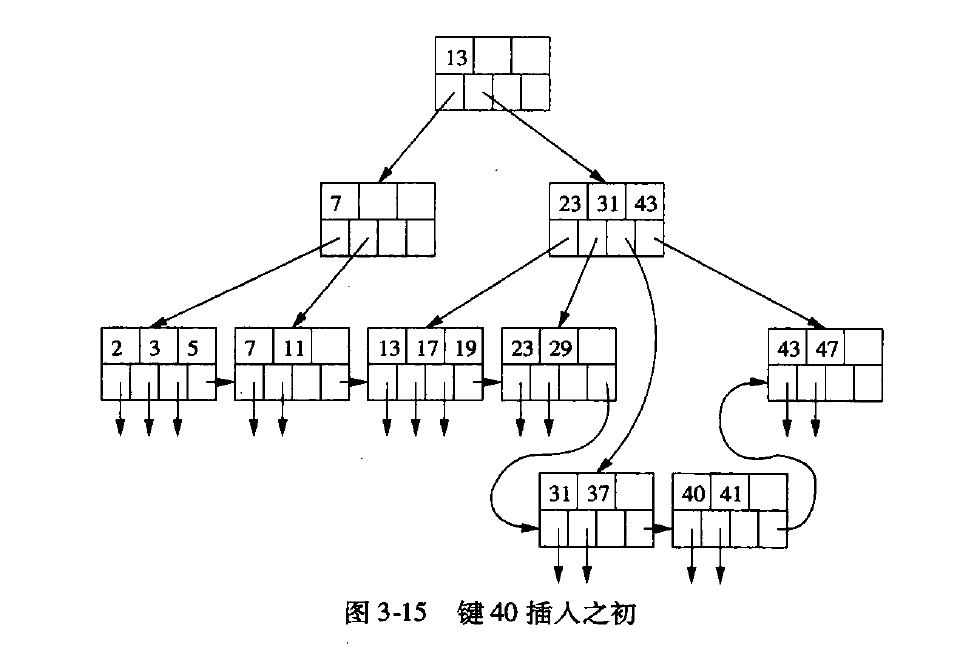
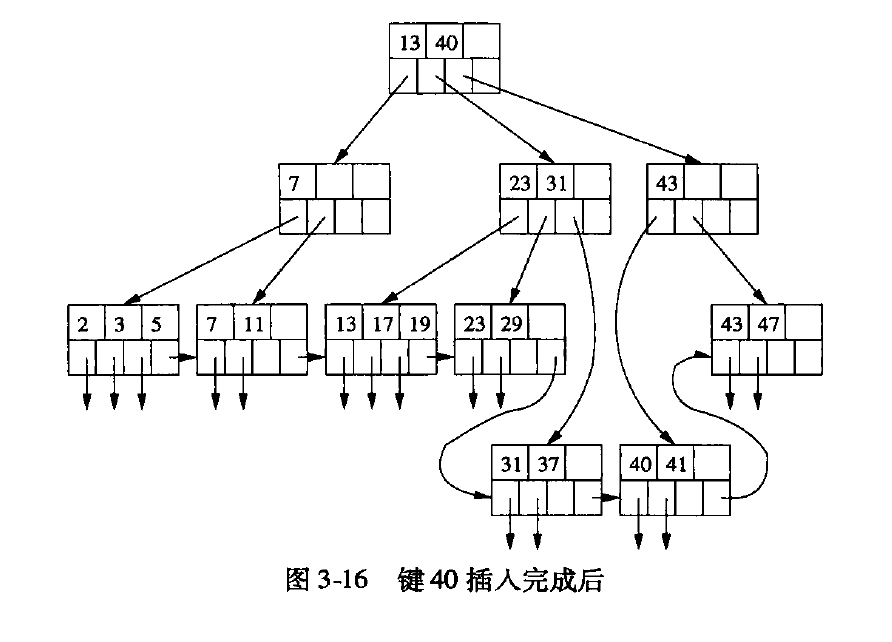
插入

  • 在合适的节点中找空间，如果节点有空间，则放入到该节点。
  • 如果合适节点没有空间， 将合适节点分裂为2个新节点， 将键分到2个新节点， 2个新节点满足有一半或超过一半的键。
  • 对于刚才分裂的节点的上一层来说，就相当于在上一层新增节点， 重复上一层的插入操作，直到根节点。

对图3-13 进行插入40节点操作， 第一步如下
image.png
第二步
image.png

删除

  • 如果删除键的节点，删除后 键还是超过最小要求，则直接删除， 不做合并操作
  •  如果删除键的节点n 的邻居节点m（是他的兄弟节点， 同一个父节点下的其他的相邻节点），可以拆一个节点过来， 则拆解一个节点过来， 并更新他们共同的父节点
  • 如果n节点的相邻节点都是最小要求， 则n节点和一个相邻节点进行合并。 然后对他们的父节点进行一个删除键操作， 重复上叙过程，直到完成删除动作。

对图3-13 进行删除7操作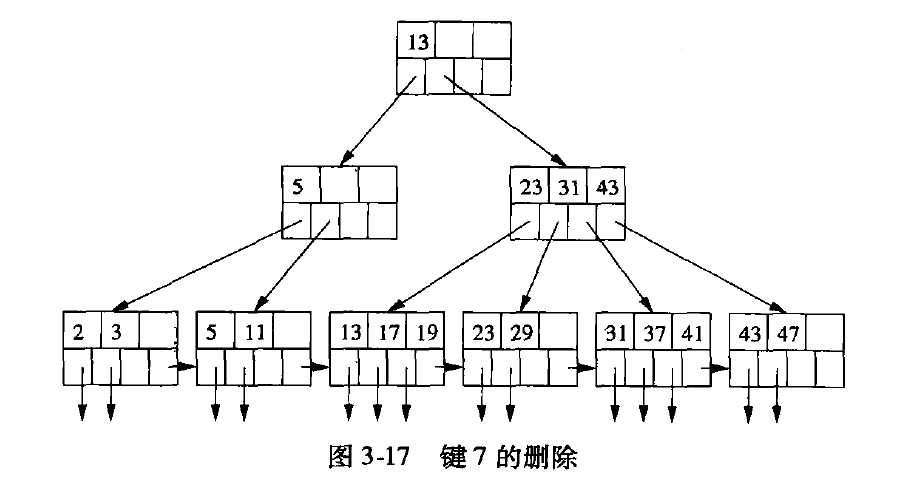
image.png
对图3-17 进行删除11的操作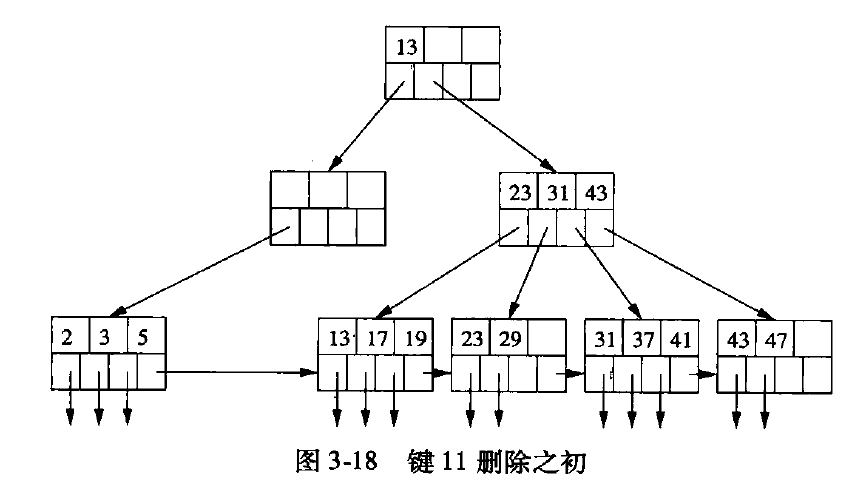
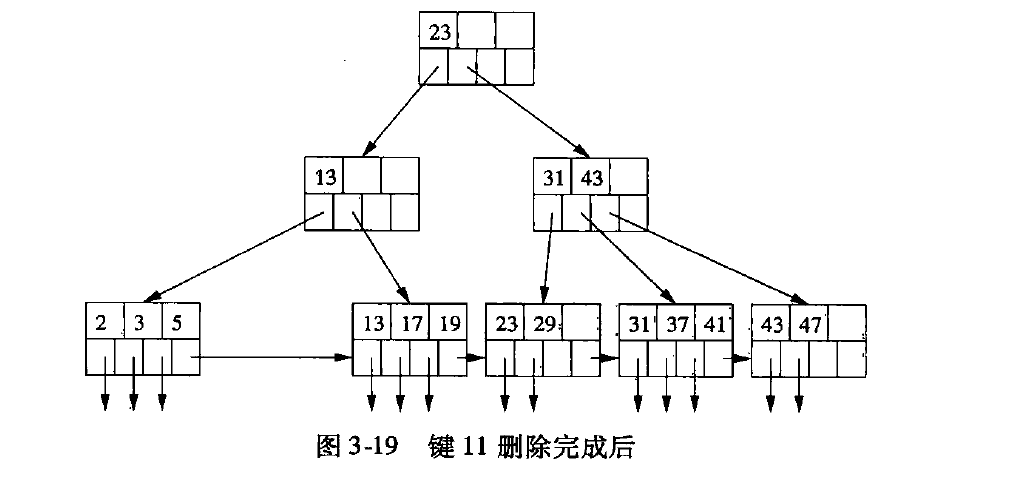
image.png
image.png

效率分析

如果每个节点容纳的键比较多， 则分裂和合并的操作就会比较少。 
访问效率， i/o效率是树的深度 + 1次（查找） /2次（插入或删除）。 

优化手段

  1. 一些b-树，删除时，并不会立刻做平衡树调整， 它会相信马上就会添加数据让它平衡， 或者大部分树发展比较平衡，节点比较多，删除不会立刻破坏平衡性。

 

hash 表

通过一个hash 函数，将键 hash到一个含有b个桶的hash 表中， hash表可能每个指针，指向一个链表
通常算法是hash(k)%b， b 通常是一个素数， 素数更有利于hash后值平均分布。
适合冲突比较少的算法， 另外不适合范围查找。

动态hash表

在静态hash表的基础上，增加

  • 增加一个中间层， 中间层存放指针，中间层是一个指针数组
  • 指针数组长度是2的幂， 当增长时， 数组长度就翻倍

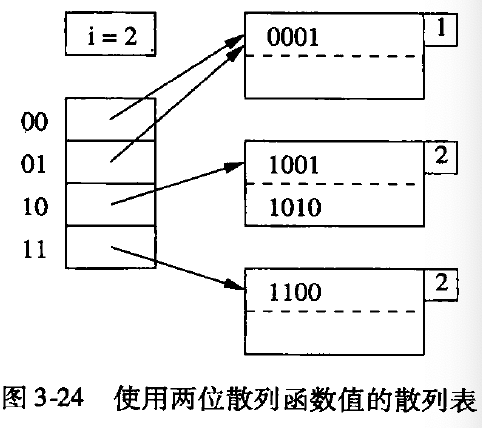
动态hash 表的插入
  • 插入一个值到目标块中， 如果目标块可存放， 则ok
  • 当目标块溢出时， 对目标块进行分裂， 取hash值后的第n位做判断位，为0， 保留在老块中，为1放到新块中。将中间层的指针重新指向新块
  • image.png
  • 缺点： 分裂的代价比较重

linear hash table

介绍

  • p: 平均每个桶能装的元素个数， 固定值
  • e： 取hash值的e位来有效
  • r： 实际元素个数
  • n： 桶个数

原则：

  • r/n <= p， 不符合时， 增加n
  • 2^(e -1) <= n < 2^e

hash表中，每个元素为（hash， key， value）
hash = hash（key） & (2^e - 1)

插入时：

  1. 当hash 值< n 时， 直接放入hash 对应的桶中
  2. 当hash 值>= n 时， hash = hash（key）& （2^ (e -1) - 1)， 放入对应的桶中。

当插入值后， 因为r在增加， 可以会破坏原则：

  1. r/n < = p, 增加n
  2. 当n增加后，如果破坏了原则 2^(e -1) <= n < 2^e， 则增加e
  3. 当e增加后， 找个空闲的时间，可以rehash一下， 对原来老的一些桶内的数据，从老的桶内挪到新的桶内。

多维索引

hash 结构

一种方式是使用网格文件（grid file）， 每一维上把空间分成条状， 按照空间2维进行组队。 
image.png

hash 结构的设计， 我觉得场景不多， 实现的效率不高， 不仔细研究了

多维树结构

  • 多键索引
  • kd树
  • 四叉树
  • r-树

多键索引

每一层是某一个索引，下一层是另外一个索引， 2个索引相互嵌套。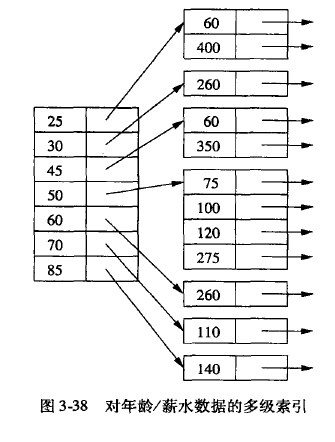 
image.png

kd 树

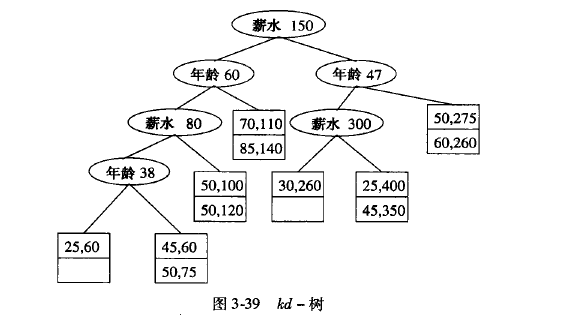
image.png
每一层都是一个索引， 每个节点都是一个值， 然后以这个值做搜索， 大于的往左边，小于的往右边，这样自动进行切分

四叉树

四叉树是2叉树的一种变种， 每个节点是一个二维的节点， 他的4个子节点代表着4个方向。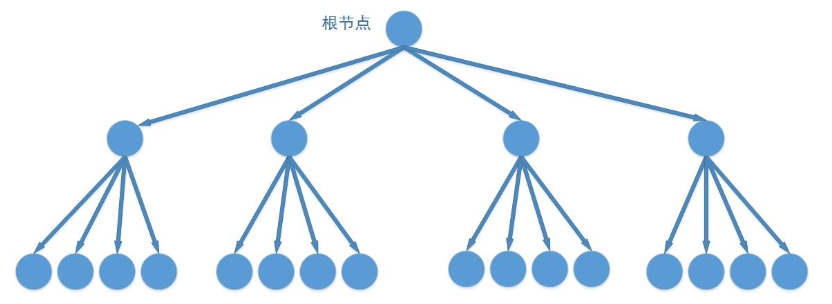 
image.png
如果支持3维， 则变成8叉树。 他不是一种平衡树。 

R 树

r树 是一种高维空间索引， 基于B树的衍生树， 是一种平衡树。 是使用非常多的一种多维空间索引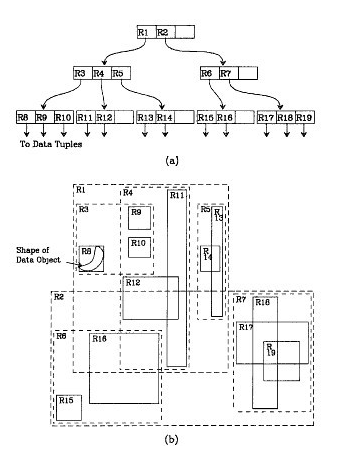
image.png
每一个节点都是一个小小的rectangle， 他的父节点就是下面几个rectangle组成起来的一个大的rectangle， 相邻的几个小rectangle合起来组成一个大的rectangle。 一个rectangle就是一个记录
原则：

  1. 除了根节点， 所有的节点至少m个rectangle， 最多M个rectangle， m=M/2， m<=n< M。
  2. 除了根节点， 他最多m<=n<M个指针，指向下一层节点
  3. 所有叶子位于同一层
  4. 叶子节点的记录是最小rectangle， 他的父节点同样是最小rectangle

  6. 叶子节点结构
  7. image.png

搜索的时候， 有一点像地图搜索， 比如，搜索杭州， 找到杭州这个rectangle， 搜索西湖区， 找到西湖区这个rectangle， 一层一层往下分解， 如果跨节点，则进行拆分。  

位图索引

位图索引， 很多时候， 都是表示这个记录在某个位置是否出现， 尤其是在一些readonly的存储上非常有用，常常标识记录是否被删除。 

举个例子
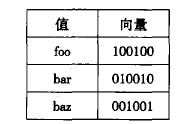
image.png
image.png

压缩位图
可以用很多算法来对位图进行压缩。 
一种思路是进行分段长度编码， 
image.png