《数据库实现》-- 第五章 查询编译器
第五章 查询编译器
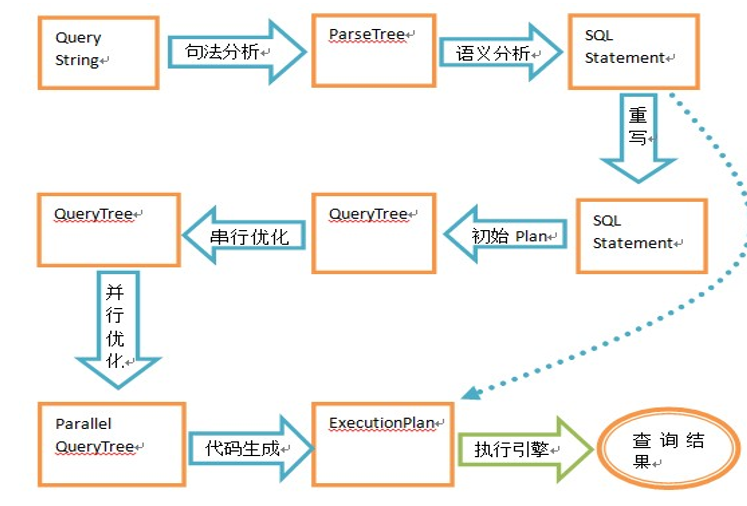
每个系统在具体执行上有一些细微的出入, 不过大致的操作差不多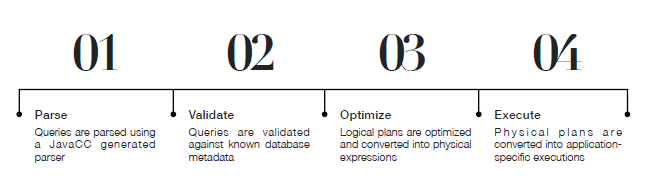
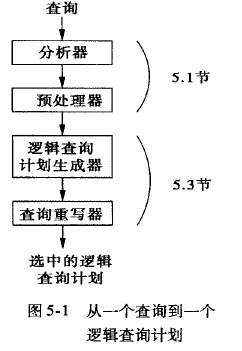
语法分析
将sql 的string 转换为语法分析树, 树的节点必须
- 原子, 它是词法成分, 如果关键字select, 关系或属性的名字
- 语法类。 用一个<>表示语法类, 比如
表示select-from-where, 表示条件,常常where之后的表达式。
查询
省略group by, having, order by, distinct, union , join等操作
省略 or、not、exist

语法树为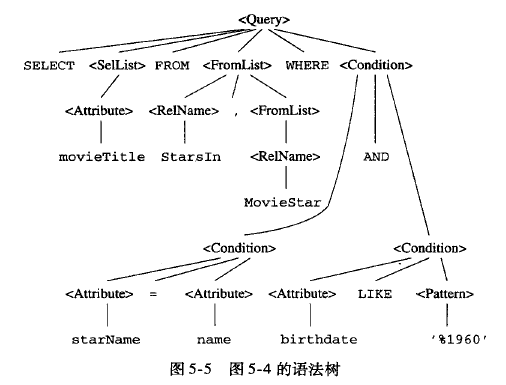
预处理
预处理要很多事情
- 语义检查
- 检查关系的使用。 from 子句出现的关系是当前关系中的关系或视图
- 视图替换为原查询树
- 检查与解析属性的使用。 select 子句或where 子句中每个属性必须是当前范围中某个关系的属性。resolve属性到关系中。 也检查二义性,如果某个属性属于2个或多个关系, 则报错
- 检查类型。



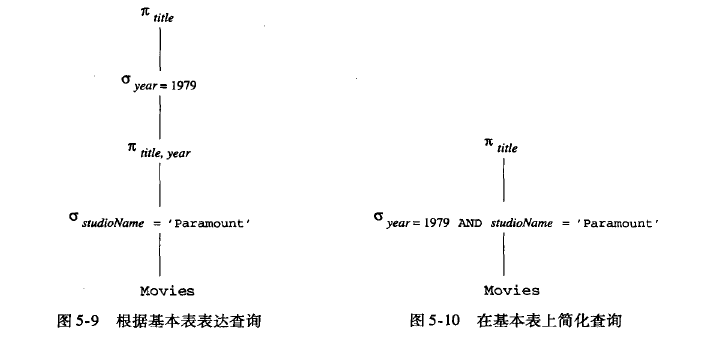
查询优化
基于代数定律的查询优化
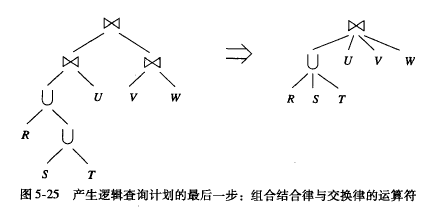
交换律和结合律
选择下推
逻辑优化里面常常进行“下推选择” 这种优化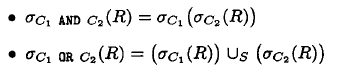
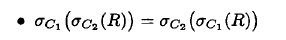
- 对于并, 下推选择到2个参数,
![image.png]()
- 对于差, 下推到第一个, 第二个可选
![image.png]() 或者
或者![image.png]()
- 对于其他, 下推到其中一个
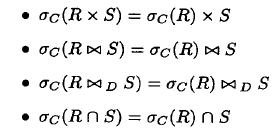
对于积或连接来说, 下推时,主要条件下推到含有属性的关系上,不要下推错了。
条件下推
有时需要将选择先上推,然后再下推到所有可能的分支。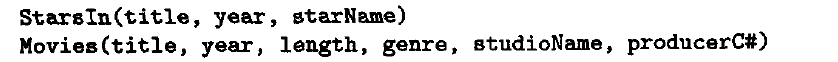
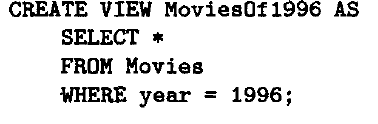
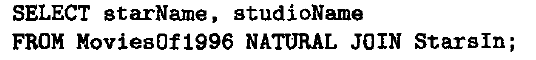
执行计划如下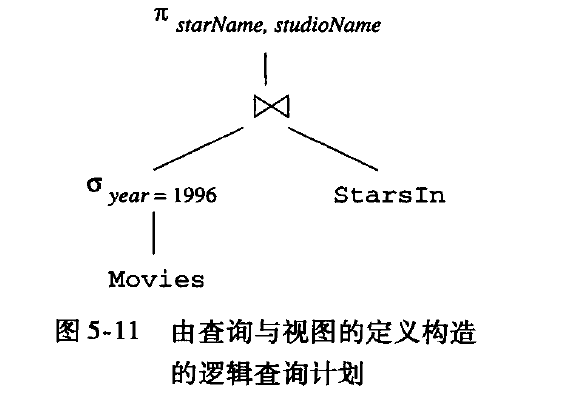
project 下推
下推project 和下推选择不一样, 保留project 在原处经常发生。
因为, 下推project 一般不改变元组数量,只是减少元组的长度。
如果project的属性,即使输入又是输出, 则成为简单的, 比如πa,b,c 这种就是简单的, 如果是π a+b->c 就是复杂的
连接和积
![image.png]() 第一个表示基于C的自然连接
第一个表示基于C的自然连接
distinct 优化
- 通常下推distinct 会有一些优化效果, 会下推到一些算子中,而不是全部算子
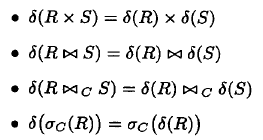
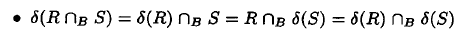
- 但一般而言, distinct 不能移入Ub, -b 或project 等运算符

- 有时把distinct 移到一个可以完全消除的位置,因为它作用到一个不含重复的关系上。
- 比如主键
- 比如对group by的结果
- 集合的一个并/交/差的结果
group by 和aggregate
- 大部分时候取决于aggregate 运算符的细节
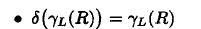
比如像distinct, min/max 不受影响, 但sum/count/avg 就会受影响

原始的plan tree 类似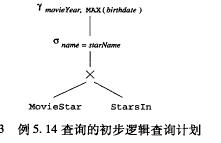
这个里面可以做几个优化
- 因为是等值join, 可以转为自然连接
- 因为最上层是做group by, 因此,可以引入distinct, distinct 对group by 不影响
- 因为最终结果只用了2个属性, 因此,可以下推projection
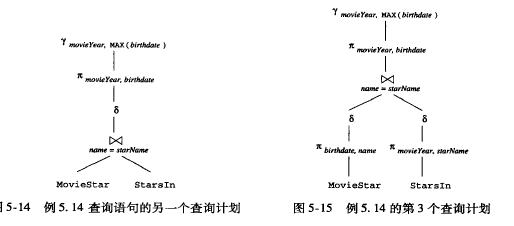
语法分析树到逻辑查询计划
- 用关系代数替换语法树上节点
- 逻辑优化
subquery
当condition中包含子查询时,引入运算符中间形式, 它介于语法树和关系代数之间,称为2参数选择 。
当对子查询进行翻译时, 这些属性后面与外部属性相比较,
- 可以将外部该属性上的条件过滤应用到子查询上
- 不需要的属性,可以project 消除
- 有一些属性可以做distinct
比如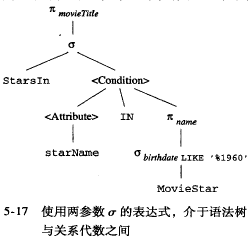 可以优化为
可以优化为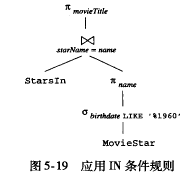
复杂subquery 优化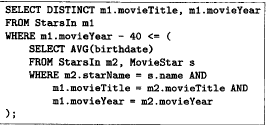
找出 影星平均年龄小于等于40岁的电影的名字和制作年份
原始语法树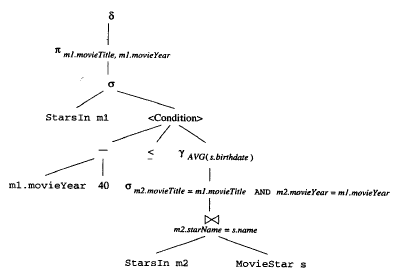
第一步优化 延迟选择
延迟选择, m1.movieTitle = m2.movieTile and m1.movieYear=m2.movieYear
- 为了 支持延迟选择, 需要对子查询的movieTitle和movieYear 进行分组, 引入group by
- 引入别名 avg(s.birthday)->abd
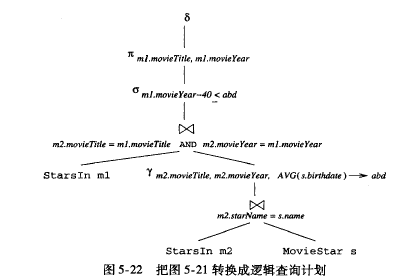
还可以做一些优化
- distinct 目前是最后执行
- starts m1 中影星名字被project 消除掉
- starts m1 的 title, year 与starts m2 的title, year 又是等职join
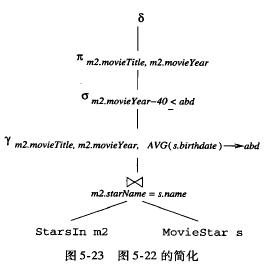
逻辑优化
- 条件过滤, 尽可能下推到子树, 当多个条件and时,可以把该条件分解并下推
- 投影也可以下推, 或者添加投影。 当有选择时, 下推投影需要小心
- distinct 有时可以消除, 或者移动到合适的地方
- 基于积的某些选择可以转换为等值join
- 将θ连接替换为自然连接, 相同名字取等值
- 增加project 消除转θ连接为自然连接时的重复属性
- 连接的条件必须是可结合的, 存在θ连接不能满足结合律
![image.png]()
cost 计算
当把逻辑计划转为物理执行计划时,可能存在多个不同的物理计划,这个时候需要对物理计划进行cost 评估。然后选择最小代价。 这种评价,称为代价枚举。
- 满足结合律和分配律的运算, 如连接、并、交、分组
- 每个运算符可能有多个实现, 比如join 有hash join和nestloop join
- 一些算子,比如scan, sort 在逻辑计划中不是显示存在,但在物理计划里面必须实例化
- 参数从一个算子传送到下一个算子的方式。 比如可以通过temp disk, 或iterator, 或内存
第一步,需要准确估计代价。 一般是经过statics 来估计。
中间表大小的估计
中间表的大小对cost 有很大的影响。
- 准确估计中间表的cost
- 易于计算
- 逻辑一致, 中间表大小估计不依赖中间表的计算方式, 比如多个连接的大小不依赖连接顺序。
很难做到3个条件同时满足,
- 不能准确估计大小时, 只要误差是稳定的, 大小估计方法能达到最佳物理计划最小计划。
project cost
- 通常project 减少record 大小,但扩展project能产生新成分,可能增加record, 这部分很难计算, 参考后续的例子。
选择 cost
selectitity,
- 通常选择一个属性等于某个值。T(s)=T(r)/v(r, a), a 是r的一个属性, v(r,a)类似cardinality, 假设V(r, a) =50, 则表示大概1/50 概率a 为某个值
- 非等值比较, 比如s=σa<10(r), 常常约定T(s)=T(r)/3 , 3分之一的满足条件
- 不等比较, 这种比较小 T(s)=T(r)(V(r, a)-1)/v(r, a)
- 多条件and 比较, 则selectivity 进行相乘
例如, 一张表r(a,b, c), s = σ a=10 and b < 20, 另T(r) = 10000, v(r, a) = 50, 则r 大概1/50 满足a =10, 1/3 满足b < 20, s = T(r)/(50 * 3), 因此结果大概是67
注意, 如果选择条件是s = σ a=10 and a > 20, 如果按照cost 计算方式应该也是67, 但实际上 应该为0, 如何防止这种错误呢, 在逻辑计划优化时候, 就应该检查条件选择, 会发现选择实际上就是false。
- 当多条件or时, 比较难计算, 一般是求和,但经常selectivity 选择出来的结果集比实际结果集还要大。 真正计算公式是, 假设r 有n个record, m1 满足条件c1, m2 个满足条件c2, s = n(1-(1- m1/n)(1-m2/n)), 1-m1/n 是不满足c1的那部分, 1-m2/n 是不满足c2 的那部分, 因此结果是如此
假设r(a, b)有 T(r) = 10000 个元组, s = σ a=10 or b < 20, 继续v(r)=50, 则s = 10000 ( 1- (1 - 1/50)(1 - 1/3)) 最后结果为3466
连接cost
这里只考虑自然连接, 另外增加2个条件, 这里只是算连接的selectivity, 但连接的cost涉及join order和io cost
- 等值连接 会转自然连接
- θ连接 可以看作积之后,进行一个条件过滤
一个初步的计算是:
1/MAX(V(r, y), v(s, y)), 就是关系r或s中, 谁的y 出现某值得概率更低,就选谁
T(r ⋈ s)= T(r)T(s)/max(v(r, y), v(s, y))
举例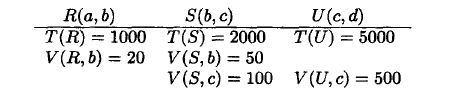
先r ⋈ s, 然后再⋈ u, (1000 * 2000/MAX(20, 50))* 5000/MAX(100, 500) = 400000
其他运算符的cost
并
selectivity 为 一般为较大者 + 较小者/2
交
selectivity 为较小者/2
差
T(r) - T(s)/2
distinct
selectivity = min(T(r)/2, T(r)/(v(r, a1) v(r, a2) xxxx))
group by & agg
计算和distinct 一样
执行plan 选择
磁盘io 受下面影响
- 物理算子
- 中间表大小
- 相似运算的排序
- 一个物理算子如何传递给下一个物理算子
histogram
histogram 常见有几种
- 等宽(singleton), 比如基于 v0 (当前已知最小值) <= V < v0+w 一个item, 下一个item 是v0 + w 《= v 《 v0 + 2w, 每一个item里面是计数器。 mysql 里面的等宽histogram 是存这个值的频率
- 等高(equi-height), 下界、上界、累积频率以及不同值的个数(Number of Distinct Value,NDV)。 每个item的下界和上届之差是相同的, 是一个等高的item。
- 最频值, 列出高频值和他的出现次数。
基于join可以直接利用histogram 判断是否有重合值。
举例:
现有最频值的histogram, r(a, b) ⋈ s (b, c), r.b histogram is
1: 200, 0 : 150, 5: 100, others : 550.
表示有200个1, 150个0, 100个5, 非0、1、5 的有550个。
s.b histogram is
0: 100, 1: 80, 2: 70, others : 250
另外假设v(r, b) = 14, v(s, b) = 13.
其中已经匹配了0, 则0的连接数 为 100 * 150 = 15000
匹配了1, 则1 的连接数为 200 * 80 = 16000
高频值2, 2的连接数 为(550/14 ) * 70 = 2750
高频值5, 5的连接数为 100 *(250/13)= 1900
其他值 连接数为 (550 * (14 -2)/14) * (250 * (13 -2)/13)/max(14, 13) = 7123
总的结果为 15000 +16000 +2750 + 1900 + 7123 = 42000 左右
如果按照默认算法 1000 * 500/MAX(14, 13) = 35174,
举例: 等宽直方图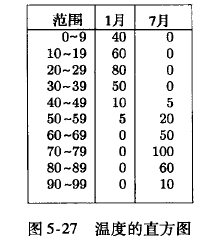

仅有2行不为0, 10 * 5/10 + 5 * 20 /10 = 15
减少启发式逻辑计划优化的代价估计
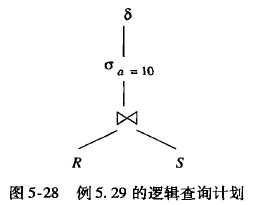 是否做下推,需要查看cost
是否做下推,需要查看cost
连接v(r, a) = 50, v(s, b) = 200, 则连接时 T(r)* T(s)/max(50, 200)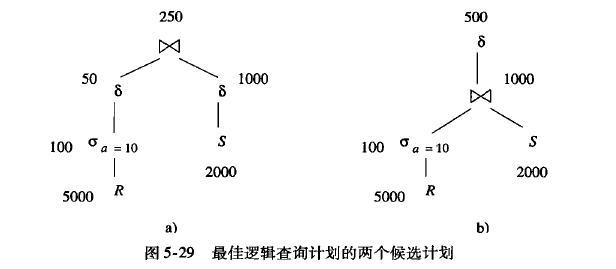
a 计划cost = 5000 + 100 + 50 + 2000 + 1000 = 8150 (把根节点排除了)
b 计划cost = 5000 + 100 + 2000 + 1000 = 8100 (把根节点排除了)
说明如果连接时, 连接匹配度比较低时, 延迟distinct 收益会更大
枚举物理计划
- 穷尽发
- 自顶向下, 对于根节点的运算的每个可能的实现,计算每种组合的代价
- 自底向上, 对于逻辑查询树的每个子表达式,计算这个子表达式的所有可能的实现。
启发式规则:
- 等值过滤时, 索引一般效率会更高
- join时,连接上有索引时, 则采用索引连接
- join时, sort-merge join 比hash join 更好。
- 3个或多个关系 并/交时, 先对小的关系进行操作。
搜索engine
枚举需要有时间限制, 比如当前找到一个计划,这个计划耗时c, 则最多搜索c的时间即可。 另外很多db, 直接有一些设置搜索时间限制,在这个限制中, 选取最优计划即可。
爬山法: 通过结合律和交换律, 对现有一个算子进行小改进, 直到找到目前不能再优化为止。
动态规划, 自底向上有明显简化, 计算大的表达式时,只考虑每个子表达式的最佳计划。 不保证整体最优,但可以获得较优,并可能最优。
system-r (selinger) 风格, 利用子表达式的某个特性来争取整体最优而不是局部最优。这种是在动态规划的基础上进行改进。 先记录每个子表达式的最优计划。 但同时记录 具有较高代价但产生的结果对较高层收益带来更多。比如,特别关注一些算子, sort、group by、join
join reorder
可能最重要的连接是一趟连接, 小表(左参数)读入内存,建立hash table, 这个过程称为build table, 大表(右参数)读入进行连接,称为probe table。
- 因为参数导致一些不同的算法, 1. 嵌套循环连接, 左参数是外层循环; 2. 索引关系, 习惯右参数带索引。
连接数量, N!
如果4张表进行连接, 则有4! = 24 中表排序方式。
左深树、右深树
右子女都是叶子的称为左深树, 类似左子女都是叶子的称为右深树。 如果既不是左深树,又不是右深树, 则称为bushy tree。
左深树有一些优点
- 将搜索空间缩小, 只需要管join order 即可, 不需要care join的位置
- join 算法比较好选择, 选择一趟连接(hash join)或嵌套循环算法(nest loop join)
- 当一个线程进行计算时(mysql),bushy tree发挥不了并行的优势
- 比较容易结合动态规划来做。
如果不是左深树, 则因为join 的位置, 需要额外倍数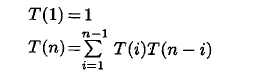
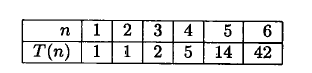
因此,如果考虑所有树的组合, 假设有6张表join, 42 *6! = 30240 种树。
- 如果用一趟连接, 选择小表在左边, 对内存消耗容易小
- 如果选择嵌套循环算法, 外层循环在左边,减少中间表的建立
通过动态规划来选择连接顺序和分组
不断迭代从局部最优进化到全局最优
- 基础, 先选取一个最优的最小集, 根据启发式规则, 选择最小的2张表, 小表为左, 其次小为右
- 迭代, 建立大小是3张表join的所有子集,选择最优, 然后扩大候选人,做4张表的最优集,直到全部表
Selinger 风格优化(搜索引擎), 不仅保持一个代价, 而是利用某些特征,在动态规划的基础上保留几个代价,后面会对这些计划都做一个迭代, 然后再进行cost estimate, 再选择一些,再迭代, 最终选择最优的一个, 搜索空间会指数级增长。
贪婪算法, 贪婪算法, 容易让搜索空间指数级增长,导致搜索十分耗时,难以承受。 动态规划或者分支限制, 是一种方式加快搜索方式。 另外常用的是启发式规则, 一旦使用启发式规则,就做了一些限制, 比如使用左深树的贪婪算法。
基于左深树的贪婪算法
物理计划
选择算子
选择算子需要考虑, 尤其是有多个条件时
- 有一个索引
- 与选择项之一的一个常量相比较
当有多个条件与时,
- 先选中带索引的
- 然后进行过滤器操作
还有一种可能是
- 直接全表扫描, 直接进行过滤器操作
不过任何时候,还是建议做cost evalutate
比如 σ x=1 AND y=2 and z < 5(r), r 在x、y、z 上都有索引,但只有z是聚集的, 其中T(R) = 5000, B(R) =200, V(R, x) =100, V(R, y) = 500
- 全表扫描, 代价为B(R), 200次磁盘io
- x 索引, T(R)/ 100 = 50 次io,
- y 索引, T(R)/V(R, y) = 10次io
- z 索引, B(R)/3 = 67 次io
整个计算下来,使用y 索引效率会最高。
join
- 一趟连接 – hash join, 会期望内存足够, 二趟连接(嵌套循环 – nestloop join),如果可以分配给左参数一些缓冲区, 可以分片。
- 当表已经排序了, 可以考虑sort-merge join
- 当多张表 基于一个属性进行join时, 前面的表join 后, 起结果是排序的, 可以考虑sort merge join
- 如果左表比较小, 右表在join 属性上有索引, 可以考虑索引连接
- 不能考虑nestloop join或sort merge join时, 可以考虑hash join。 扫描的次数取决于较小的参数。
pipeline 和materize
pipeline 有更好的性能,更容易进行并行,节省磁盘io,但对内存的消耗更大, 需要共享内存。
materize 将结果物化到磁盘上, 消耗更多的磁盘io。
一元操作很适合流水线, 比如选择和投影, 流水线时,非常容易调用getnext 从而进行下一层的迭代。
二元流水线, 比如join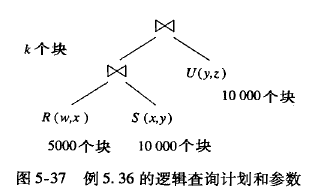
假设,
- r 5000个块, s、u 各10000个块
- 共有101 个缓冲块
- 中间结果使用k个块
这种情况采用二趟hash 连接(hybrid hash join),
因为有101 个缓冲块, 整除2 (因为有下一级流水,所以一个build hash table, 一个output hash table, 如果没有下一级流水, 则结果直接output 到网络)再向下取整, 则有50个块, 则按照 一个桶50个块来设计 hybrid hash join
一个桶50块, 则表r 切分100块, 每个桶50块, 从s 进行读入需要消耗一个缓冲块, 下一级流水线从u进行读入需要消耗一个内存块, 第一层join, build hash table消耗50块, 则第一层的output 只能为49块。 当第一层join的49块缓冲块被填满时, 会驱动进行下一层的join。如果一个桶做完了join, 第一层的output hash table依旧没有满,则load 第二个桶
- 当中间表 块小于等于 49时, 则第二级的join, 直接使用内存hash join,全表load。 总io 次数
- (5000 + (5000 -50)) + ( 10000 + (10000 - 50)) +10000 = 40000 -100
- 当中间表的块 》49时, 第二层join 已经不适合nestloop join, 期待hybrid hash join
- (5000 + (5000 -50)) + ( 10000 + (10000 - 50))
- ((k -49)* 2(读写) +49) + (10000 +10000 -49)
- 合计50000 + 2 *k - 200 左右
物理算子
逻辑树叶子的物理算子
- Tablescan(R)
- SortScan(R)
- IndexScan(R, C), 一种是全索引扫描, 一种类似过滤条件快速定位(比如利用B+ 树等)
选择的物理算子
- Filter(C)
排序的物理算子
- SortScan(r, l)
- 在连接或分组 运算中, 常常使用sort
- 可以使用一个物理算子sort 对没有排序的关系进行排序
- order by 产生的算子, 往往在物理计划的顶端
其他算子
- 算法基于的策略, 基于排序, 散列或索引
- 用于遍历,需要考虑是使用一趟遍历算子, 两趟遍历, 还是三趟遍历算子
- 考虑内存消耗量
物理算子的排序
就是执行的顺序,
- 有可能是使用迭代器流水线进行操作
- 也有可能使用不同节点交替执行 (比如bushy tree)
- 如果涉及中间表或spill或稍微再检索 执行物化
规则:
- 在物化处拆解子树, 子树可以一次一个被执行
- 一般逻辑, 从下至上, 从左到右
- 在子树执行过程中, 使用迭代器pipeline 进行执行
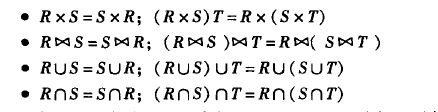
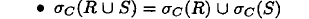
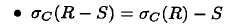 或者
或者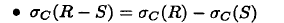
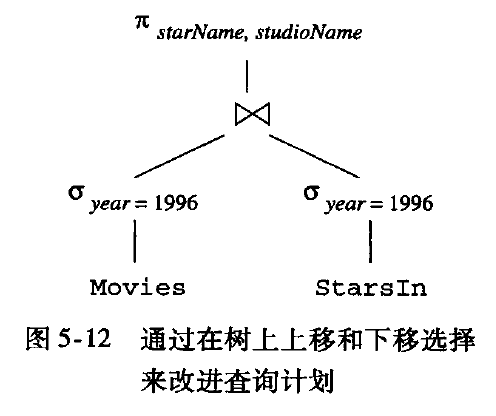
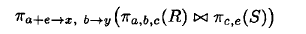
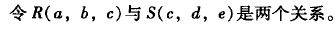
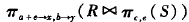

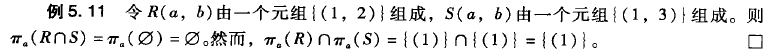

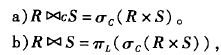 第一个表示基于C的自然连接
第一个表示基于C的自然连接